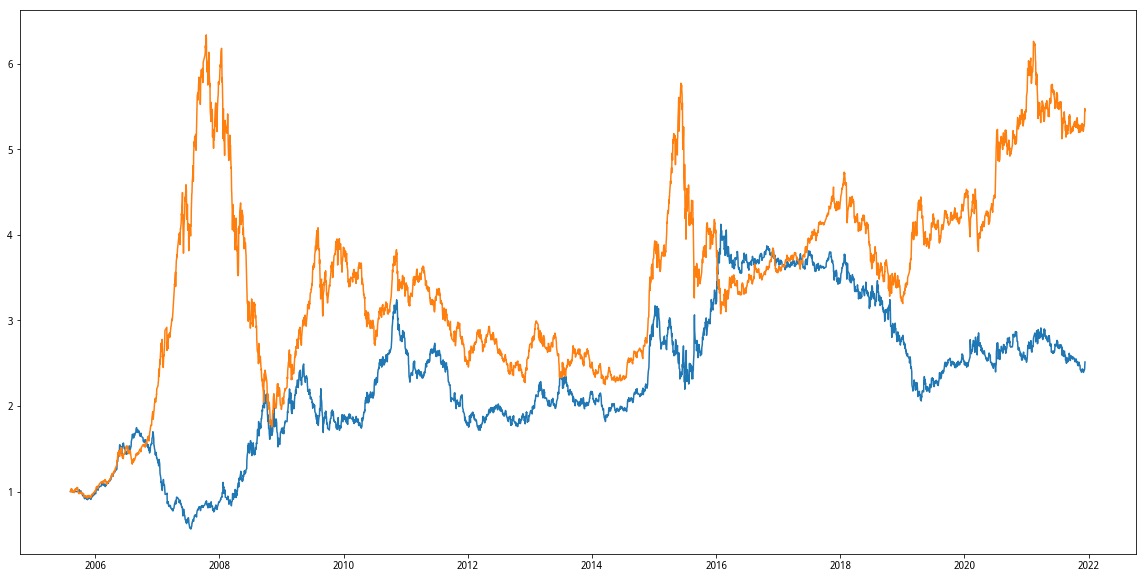
研究思路
顺势指标CCI由唐纳德拉姆伯特所创,是通过测量股价的波动是否已超出其正常范围,来预测股价变化趋势的技术分析指标。由于选用的计算周期不同,顺势指标CCI也包括日CCI指标、周CCI指标、年CCI 指标以及分钟CCI指标等很多种类型。经常被用于股市研判的是日CCI指标和。虽然它们计算时取值有所不同,但基本方法一样。
计算方法:
第一步:
\(TP_i = \frac{H_i+L_i+C_i}{3}\)
第二步,计算最近n日TP的移动平均:
\(MATP(n)_t = \frac{1}{n}\sum_{i=1}^nTP_{t-i+1}\)
第三步,计算最近n日TP的一阶均差:
\(meanDev(n)_t = \frac{1}{n}\sum_{i=1}^n|TP_{t-i+1}-MATP(n)_t|\)
第四步:
\(CCI(n)_t = \frac{TP_t-MATP(n)_t}{α*meanDev(n)_t}\)
其中α一般取0.015,而n取20。 CCI指标没有运行区域的限制,在正无穷和负无穷之间变化。但是,和所有其 它没有运行区域限制的指标不一样的是,它有一个相对的技术参照区域:+100 和-100。按照指标分析的常用思路,CCI指标的运行区间也分为三类:+100以上为超买区,-100以下为超卖区,+100到-100之间为震荡区。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 from jqdata import *import numpy as npimport pandas as pdimport matplotlib.pyplot as plt'2005-09-01' '2021-12-12' 20 0.015 '000300.XSHG' def cal_meandev (tp,matp ):1 )*[np.nan]for i in range (len (tp)-n+1 ):abs (tp[i:i+n]-matp[i+n-1 ])))return np.array(mean_dev)1 )0 ]def get_data (start,end,n,a,index ):'close' ,'high' ,'low' ] )'tp' ] = (df['close' ]+df['high' ]+df['low' ])/3 'matp' ] = df['tp' ].rolling(n).mean()'tp' ],df['matp' ])'mean_dev' ] = mean_dev'cci' ] = (df['tp' ]-df['matp' ])/(a*df['mean_dev' ])return df10 )
close
high
low
tp
matp
mean_dev
cci
2021-11-29
4851.42
4858.53
4818.71
4842.886667
4868.679833
24.134167
-71.249381
2021-11-30
4832.03
4871.25
4810.22
4837.833333
4868.088500
24.725500
-81.576151
2021-12-01
4843.85
4844.52
4823.93
4837.433333
4868.557000
24.257000
-85.538653
2021-12-02
4856.16
4866.85
4830.32
4851.110000
4868.155500
24.658500
-46.084177
2021-12-03
4901.02
4901.02
4853.35
4885.130000
4869.515833
24.930833
41.753295
2021-12-06
4892.62
4943.90
4888.69
4908.403333
4872.570167
25.635500
93.186315
2021-12-07
4922.10
4934.10
4895.22
4917.140000
4876.159333
26.144400
104.498265
2021-12-08
4995.93
4995.93
4915.79
4969.216667
4884.487000
25.891000
218.170192
2021-12-09
5078.69
5114.50
4999.41
5064.200000
4894.256833
34.613200
327.318608
2021-12-10
5055.12
5060.06
5035.81
5050.330000
4902.226667
43.047667
229.363316
策略构造
标的为沪深300指数日频数据(2005-09-01至2019-07-12)
策略表现
双边交易策略
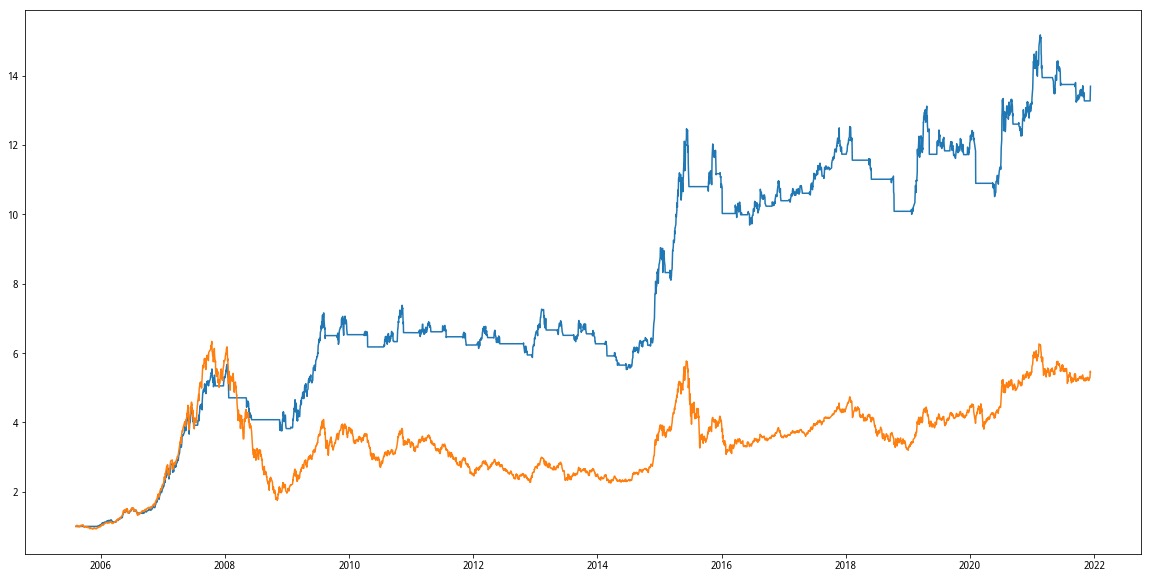
我们可以看出,双边交易策略的收益主要来自于几次牛市行情,在震荡行情中的表现普通,而这也是一般趋势类择时策略的特点。策略总收益7.68,夏普比率0.70,表现可以说不错。但是最大回撤达到了47%,这是我们不希望看到的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 100 def gen_signal (cci,threshold ):0 ]for i in range (n,len (cci)):if cci[i]>threshold and cci[i-1 ]<threshold:1 )elif cci[i]<-threshold and cci[i-1 ]>-threshold:1 )else :0 )return np.array(signal)def gen_position (signal,short ):0 ]if short:1 else :0 for i in range (1 ,len (signal)):if signal[i] == 1 :1 )elif signal[i] == 0 :1 ])else :return np.array(position)def cal_ret (df ):0 ]for i in range (n,len (df)):'position' ][i-1 ]*df['index_ret' ][i])return retdef cal_cum_ret (ret ):1 ]for i in range (len (ret)-1 ):1 ]*(1 +ret[i]))return cum_retdef back_test (df,threshold,short,plot=True ):'index_ret' ] = np.concatenate(([np.nan],np.array(df['close' ][1 :])/np.array(df['close' ][:-1 ])))-1 'signal' ] = gen_signal(df['cci' ],threshold)'position' ] = gen_position(df['signal' ],short)'ret' ] = ret'总收益' ]=cum_ret[-1 ]-1 '日胜率' ] = len (ret[ret>0 ])/(len (ret[ret>0 ])+len (ret[ret<0 ]))min (cum_ret/max_nv-1 )'最大回撤' ]=mdd'夏普比率' ]=ret.mean()/ret.std()*np.sqrt(240 )0 ])if plot:1 ,figsize=(20 ,10 ))'策略表现' ,fontsize=18 )'close' ]/df['close' ][0 ])'CCI策略' ,'HS300' ],fontsize=14 )return sum_dfTrue )
总收益
日胜率
最大回撤
夏普比率
0
5.326277
0.526689
0.471381
0.557055
双边交易策略敏感性分析
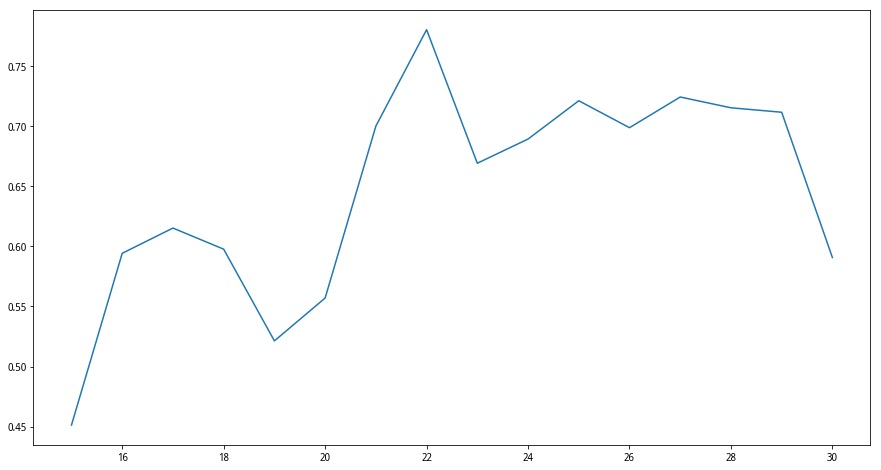
我们通过寻找夏普比率最大的参数n来优化参数,最优参数为22。
1 2 3 4 5 6 7 8 9 list (range (15 ,31 ))for n in ns:True ,False )'夏普比率' ][0 ])15 ,8 ))
[<matplotlib.lines.Line2D at 0x7f882d2c7c88>]
1 2 3 22 ,a,index)True ,True )
总收益
日胜率
最大回撤
夏普比率
0
10.360562
0.534653
0.502721
0.693407
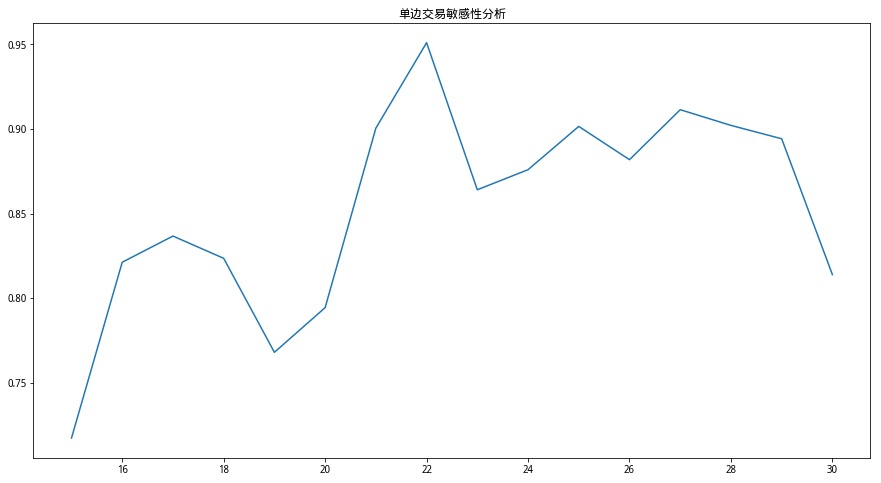
单边交易策略表现
通过类似的参数优化方法,我们得到单边交易策略的最优参数22。 单边交易策略的总收益低于双边交易,为8.37,但收益更稳定:最大回撤仅为29%,夏普比率达到0.96。
1 2 3 22 ,a,index)False ,True )
总收益
日胜率
最大回撤
夏普比率
0
9.677065
0.564979
0.338632
0.888496
1 2 3 4 5 6 7 8 9 10 list (range (15 ,31 ))for n in ns:False ,False )'夏普比率' ][0 ])15 ,8 ))'单边交易敏感性分析' )
[<matplotlib.lines.Line2D at 0x7f882e479780>]
从该指标的设计来看,在一般常态行情下,CCI指标不会发生作用。当CCI扫描到异常股价波动时,也就是当CCI突破+/-100时,可以抓住市场趋势。但是在上涨/下跌行情中出现短暂反方向运动时,该策略会出现误判,又因为策略的信号频率不高,也因此带来比较大的回撤。
双边交易策略表现
优化后的双边交易策略总收益大幅提升,达到25.49,夏普比率也达到0.99。策略成功避开了几次熊市的回撤。但是在2012-2014这一段震荡行情中,策略遭遇了52%的大幅回撤,这是优化策略更高的换手率造成的:高换手率可以避开熊市的回撤,但在震荡市中,过高的换手同样会造成回撤。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 def gen_signal_2 (cci,threshold,m ):0 ]0 for i in range (n,len (cci)):if cci[i]>threshold and cci[i-1 ]<threshold:1 )elif cci[i]<-threshold and cci[i-1 ]>-threshold:1 )elif cci[i]<threshold and cci[i-1 ]>threshold:try :if up_list[-1 ]<i-m:0 ) else :1 )except :0 )elif cci[i]>-threshold and cci[i-1 ]<-threshold:try :if down_list[-1 ]<i-m:0 ) else :1 )except :0 )else :0 )print (len (signal))return np.array(signal)def back_test_2 (df,threshold,m,short,plot=True ):'index_ret' ] = np.concatenate(([np.nan],np.array(df['close' ][1 :])/np.array(df['close' ][:-1 ])))-1 'signal' ] = gen_signal_2(df['cci' ],threshold,m)'position' ] = gen_position(df['signal' ],short)'ret' ] = ret'总收益' ]=cum_ret[-1 ]-1 '日胜率' ] = len (ret[ret>0 ])/(len (ret[ret>0 ])+len (ret[ret<0 ]))min (cum_ret/max_nv-1 )'最大回撤' ]=mdd'夏普比率' ]=ret.mean()/ret.std()*np.sqrt(240 )0 ])if plot:1 ,figsize=(20 ,10 ))'close' ]/df['close' ][0 ])return sum_df20 ,a,index)7 ,True )
3975
总收益
日胜率
最大回撤
夏普比率
0
1.513961
0.501523
0.678913
0.342679
单边交易策略表现
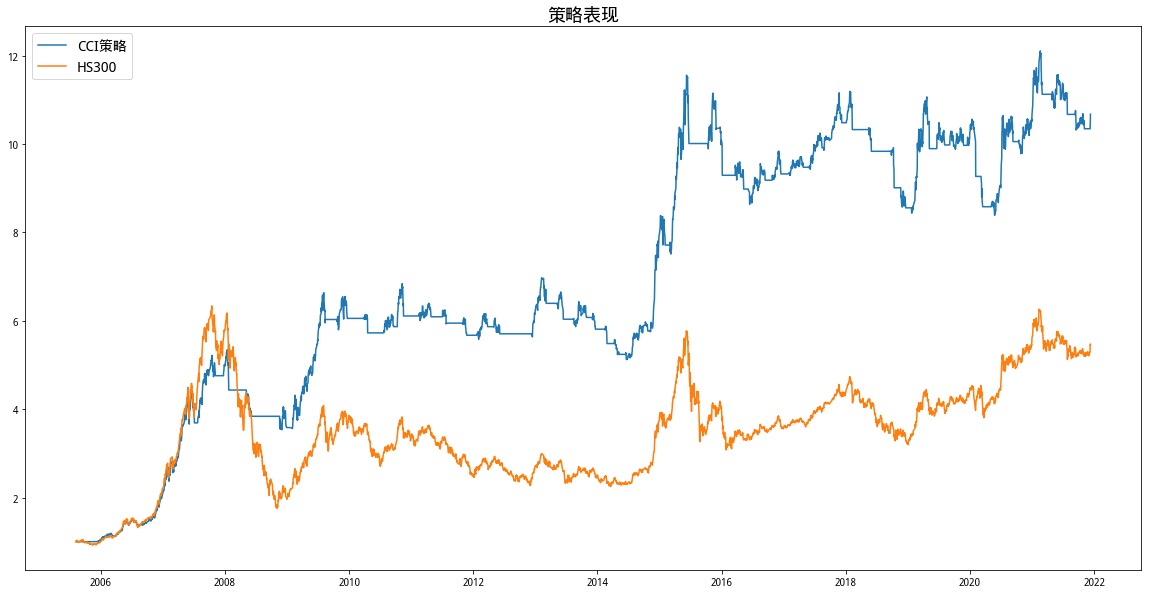
我们进一步考察优化后的单边交易策略。一般来说,单边交易策略的收益回比双边交易策略低,但它的收益会更稳定。优化的单边交易策略总收益同样大幅提升,达到12.65,夏普比率达到1.12。但其同样没能避开2012-1014年的这一段回撤,最大回撤达到40%。
1 2 3 20 ,a,index)False ,False )
3975
总收益
日胜率
最大回撤
夏普比率
0
12.694457
0.567757
0.338632
0.984271
研究结论
总的来说,CCI可以捕捉到趋势行情。普通的CCI择时策略能捕捉到长期趋势,但对于突然的趋势反转反应不足,会在熊市遭受回撤。而优化后的CCI策略捕捉短期趋势的能力更强,但会在横盘震荡行情由于频繁换仓而遭遇较大的回撤。。但是不管哪种策略,指标的钝化,以及脉冲式的行情两点造成的错判都是不可避免的。那么按照这个思路,对于指标钝化未来我们将加入与之互补的指标加以配合,而对于脉冲式行情,我们考虑运用高频数据去捕捉“瞬间”的机会。
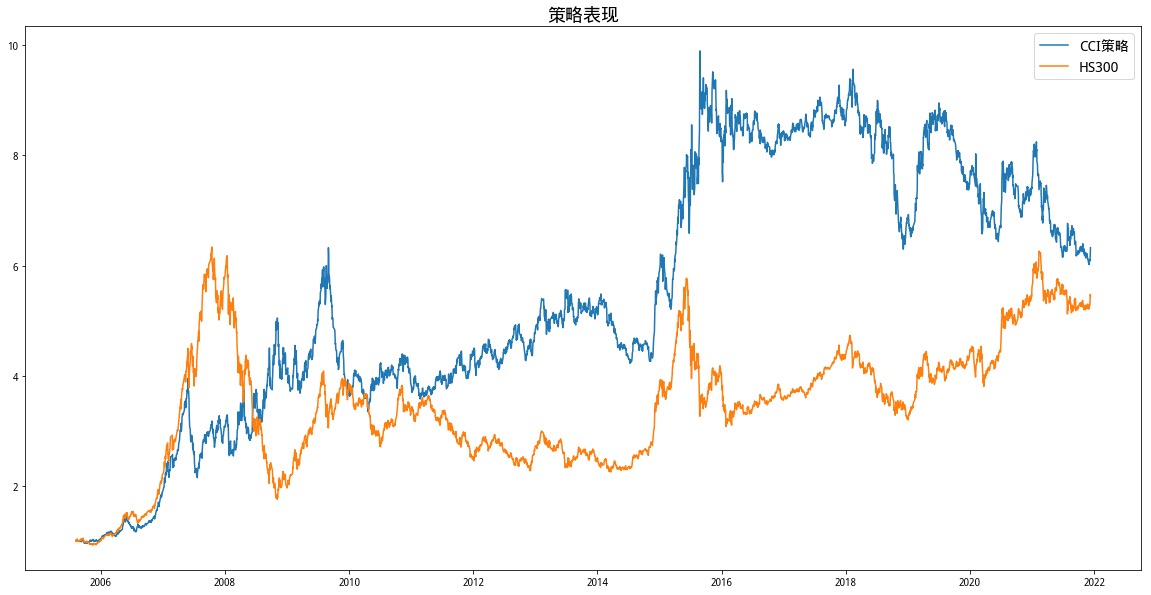
 优化后的策略成功避开了2009-2010年这一段时间的回撤,但仍未避开2018年底和2019年初的大回撤。但总的来说,相对于未优化的策略还是有所改善,总收益达到11.55,夏普比率0.80。
优化后的策略成功避开了2009-2010年这一段时间的回撤,但仍未避开2018年底和2019年初的大回撤。但总的来说,相对于未优化的策略还是有所改善,总收益达到11.55,夏普比率0.80。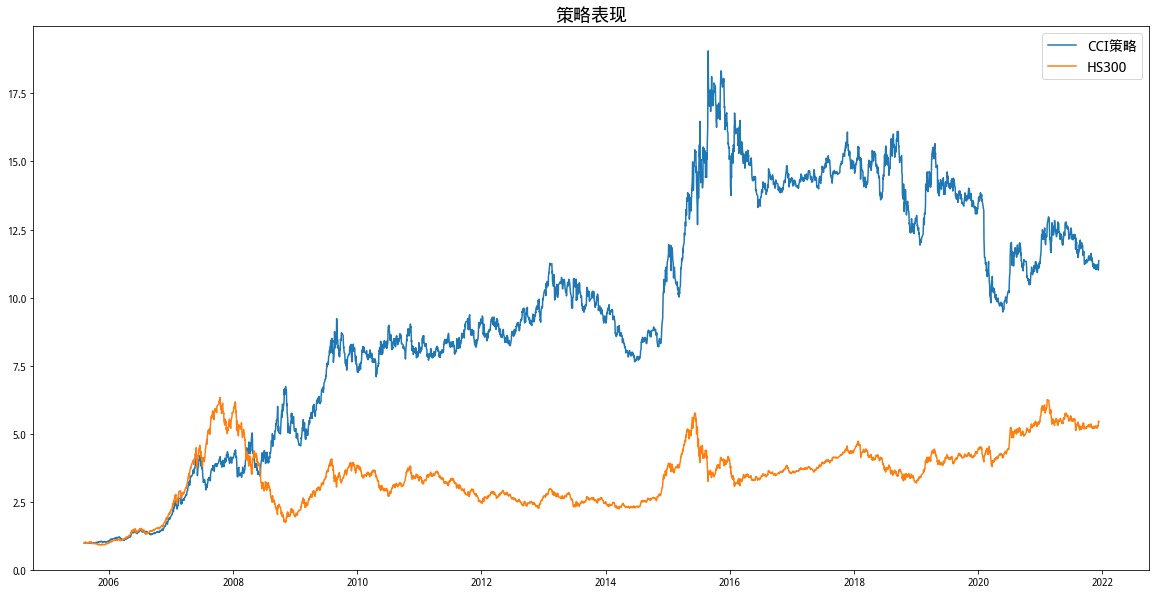
 ## 优化的CCI策略
## 优化的CCI策略